A better path to pruning large language models

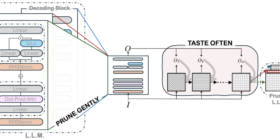
A better path to pruning large language models

⋅

A better path to pruning large language models A new philosophy for developing LLM architectures reduces energy requirements, speeds up runtime, and preserves pretrained-model performance. Conversational AI Kai Zhen August 08, 02:06 PM August 09, 11:22 AM In recent years, large language models (LLMs) have revolutionized the field of natural-language processing and made significant contributions to computer vision, speech recognition, and language translation. One of the keys to LLMs effectiveness has been the exceedingly large datasets theyre trained […]

Ver mais

Liked Liked
Byte magazine artist Robert Tinney, who illustrated the birth of PCs, dies at 78

Byte magazine artist Robert Tinney, who illustrated the birth of PCs, dies at 78

⋅

On February 1, Robert Tinney, the illustrator whose airbrushed cover paintings defined the look and feel of pioneering computer magazine Byte for over a decade, died at age 78 in Baker, Louisiana, according to a memorial posted on his official website. As the primary cover artist for Byte from 1975 to the late 1980s, Tinney became one of the first illustrators to give the abstract world of personal computing a coherent visual language, translating topics like artificial intelligence, […]

Ver mais

Liked Liked

What is the AGI in Offensive Security ?

⋅

arXiv:2601.19968v1 Announce Type: new Abstract: What is the AGI in Offensive Security? One can break it down into two questions : (1) any offensive security tasks could be reduced into symbolic language manipulation (language representation + reasoning), (2) powerful language model (LLM) are enough to “deal with” any symbolic language manipulation. This paper can formally model a target system as a state machine and a hacker as an interactive symbolic agent. And it shows that every interaction in […]

Ver mais

Liked Liked

[P] cv-pipeline: A minimal PyTorch toolkit for CV researchers who hate boilerplate

⋅

To all DS and ML researchers If someone got tired of copy-pasting the same data loading, training loops, and export code for every CV project. So I built a toolkit that handles the boring stuff. What it does: from cv_pipeline import quick_train, analyze_dataset, export_model # Analyze your dataset analyze_dataset(“./my_images”) # Train (one line) model, history = quick_train(“./my_images”, model=”efficientnet_b0″, epochs=10) # Export for deployment export_model(model, “model.onnx”, format=”onnx”) Key features: Data loading – Point to a folder, get DataLoaders. Handles […]

Ver mais

Liked Liked

Contextual Trust Evaluation for Robust Coordination in Large Language Model Multi-Agent Systems

⋅

Large Language Model (LLM)-based multi-agent systems have emerged as a promising paradigm for tackling complex tasks that exceed individual agent capabilities. However, existing approaches often suffer from coordination inefficiencies, a lack of trust mechanisms, and suboptimal role assignment strategies. This paper presents a novel trust-aware coordination framework that enhances multi-agent collaboration through dynamic role assignment and context sharing. Our framework introduces a multi-dimensional trust evaluation mechanism that continuously assesses agent reliability based on performance history, interaction quality, and […]

Ver mais

Liked Liked

Introducing Provable Randomness in Beldex Consensus with Verifiable Random Functions

⋅

The concept of Verifiable Random Functions (VRFs) was first introduced over two decades ago in 1999, by cryptographers Silvio Micali, Michael O. Rabin, and Salil Vadhan.  Back in the day, it was considered a generational breakthrough in cryptography. It gave cryptographers a way to produce randomness that anyone can verify, yet no one can predict or manipulate. Today, the same VRFs, with a little bit of modification, are at the center of modern blockchain networks, ensuring fair, secure, […]

Ver mais

Liked Liked

Flow Matching for Offline Reinforcement Learning with Discrete Actions

⋅

Generative policies based on diffusion models and flow matching have shown strong promise for offline reinforcement learning (RL), but their applicability remains largely confined to continuous action spaces. To address a broader range of offline RL settings, we extend flow matching to a general framework that supports discrete action spaces with multiple objectives. Specifically, we replace continuous flows with continuous-time Markov chains, trained using a Q-weighted flow matching objective. We then extend our design to multi-agent settings, mitigating […]

Ver mais

Liked Liked

Reflections

⋅

The second birthday of ChatGPT was only a little over a month ago, and now we have transitioned into the next paradigm of models that can do complex reasoning. New years get people in a reflective mood, and I wanted to share some personal thoughts about how it has gone so far, and some of the things I’ve learned along the way. As we get closer to AGI, it feels like an important time to look at the […]

Ver mais

Liked Liked

Any tutorials for Imitation Learning

⋅

Hey folks, I’m trying to get into Imitation Learning, but honestly most of what I find are dense papers 😅 I’m looking for tutorial-style resources….blogs, courses, lecture videos, or walkthroughs, that explain IL concepts clearly instead of jumping straight into theory. If you know any good resources that helped you understand things like Behavior Cloning, DAgger, or GAIL, please share! Papers are fine, but I’d really appreciate something more beginner-to-intermediate friendly. Thanks 🙏 submitted by /u/GraciaMad [link] [comments]

Ver mais

Liked Liked

Load More

↑

Digitado © 2025